A Reversible Synthetic Rotary Molecular Motor
José V. Hernández, Euan R. Kay and David A. Leigh, Science, 306, 1532-1537 (2004).
School of Chemistry, University of Edinburgh, Group Website, Full Article.
Scientists at the University of Edinburgh have made the first reversible synthetic molecular motor. Like the molecular motors found throughout biology (e.g. to move muscles, power mechanical motion and pump ions), the synthetic motor works by capturing random displacements that occur during Brownian motion and directionally releasing them. The system consists of a small ring mechanically locked onto a larger ring – a [2]catenane. The small ring can be made to move around the larger one by applying a series of chemical reactions. Remarkably, the sense of rotation (clockwise or counter-clockwise) is governed solely by the order in which these reactions are carried out.
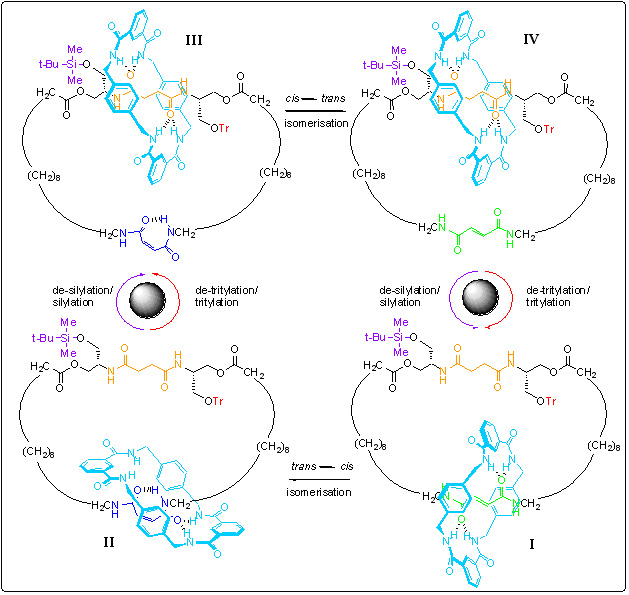
Scheme 1.Operation of a reversible synthetic molecular motor. The motor consists of two mechanically interlocked rings; the larger ring can be considered a track for the smaller ring (shown in blue) to move around. The smaller ring starts on the green ‘station’ (the bottom right structure, I). Shining with ultra-violet light causes a chemical reaction that switches off the ‘stickiness’ of the station meaning the blue ring wants to move to the orange station, however it is unable to do so because bulky groups (shown in purple and red) block both routes to the orange station (structure II). Removing, and then replacing, of a blocking group allows the blue ring to move to the orange station by biased Brownian motion (structure III). If it is the purple group that is removed/re-attached, the blue ring moves clockwise to get to the orange station; if it is the red group that is removed/re-attached it moves counter-clockwise. In order to complete the 360 degree rotation of the blue ring, the first chemical reaction is reversed (using a chemical catalyst, piperidine) to generate structure IV. Now removal/re-attachment of the second blocking group allows the blue ring to return to its original position (structure I).
Being able to make practical molecular motors is a prerequisite for future visions of a 'working synthetic nanotechnology', whatever that turns out to eventually be. Perhaps the best way to appreciate the impact that molecules that can 'mechanically power' themselves or other molecules or ions is to realise that nature uses such molecules extensively. In fact, virtually every biological process exploits mechanical motion, from the cis-trans isomerisation of retinal (which produces the visual signal) to rotary motor enzymes like ATPase (which harness and store chemical power in the cell) to muscles (which produce macroscopic power from mechanical molecular motion) and ion pumps. In contrast, despite all the fantastic technology man has developed, we do not make use of the controlled motion of molecular components at all (the one notable exception being liquid crystals). The molecular motor reported in Science is a step towards changing that. In addition to being the first synthetic motor that can rotate in either direction (beautiful rotary motors made by Ben Feringa's group in Groningen, Ross Kelly at Boston College in the USA and a previous example made by the Edinburgh group, are each only capable of rotating in a single direction), one of the most important outcomes of the latest system is that it explains what features are necessary for the design of rotary motors - i.e. what the minimum requirements are. This will aid scientists to design improved systems that are more practical than these first generations (which are slow - rotate on the order of hours - and require multiple chemical inputs to be applied for each rotation).
How to Design a Molecular Motor
One of the most important features of the motor shown in Scheme 1 is that it demonstrates what is required to achieve directional rotation in molecular systems – i.e. how to make a rotary molecular motor. The [2]catenane is a minimalist design for a rotary motor - every piece of functionality is necessary to achieve directionality of motion. The minimal features required for any molecular motor can be understood by considering the following three systems:
A – The role of Brownian Motion (the random motion which allows the system to surmount small kinetic barriers and seek the lowest energy arrangement i.e. to move to equilibrium)
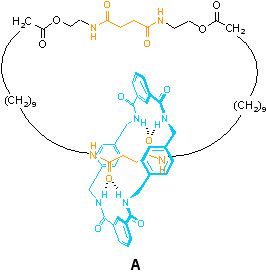
In [2]catenane A, the large macrocycle contains two binding sites, or ‘stations’ (shown in orange), for the smaller ring. When the blue ring is at those sites, hydrogen bonds (relatively weak, but directional bonding interactions) are formed between the two rings. At all temperatures above absolute zero, however, molecules are subject to thermal fluctuations. The result is Brownian motion – constant, random motion of molecules and their components. This thermal energy is sufficient to break the relatively weak hydrogen bonding interactions between the two rings and allow the small macrocycle to move (it is still constrained to follow the path of the large macrocycle, of course). The small macrocycle is thus able to explore the full circuit of the larger ring and can move between the two stations.
So, although movement of the blue ring occurs in this system, it is completely random; there is no net transport of small rings from one station to the other or in one particular direction (clockwise or counter-clockwise). Brownian motion alone is not sufficient to achieve directionality of motion (this was famously discussed by Richard Feynman in the ‘Feynman Lectures on Physics’ in 1963).
B – The need for asymmetric kinetic barriers in the possible directions of motion
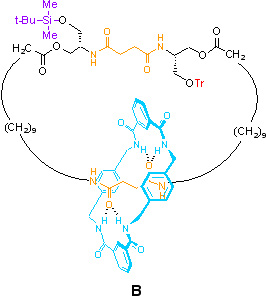
In [2]catenane B, bulky ‘gate’ groups (in the form of a silyl ether and a trityl ether) allow us to select which path the small ring takes around the large one (i.e. they control of the kinetics for transport of the small ring). If all the small rings start off on the bottom station, removal of the silyl ether will result in a net clockwise rotation (as drawn above) for 50% of the rings, so as to give an equal distribution of rings between the stations at equilibrium. Once the silyl group is reinstated, the large macrocycle is restored to its original composition. So here we do have net unidirectional motion – why is [2]catenane B then not a molecular motor?
The problem is that one cannot achieve repetitive directionality of motion with such a system. The next step would be to remove the trityl ether, so that Brownian motion can continue in a clockwise sense. So, half of the rings on the top station (25% of the total) will indeed undergo another 180o clockwise transition, to complete a total 360o cycle. But of course, half of the rings on the bottom station (again, 25% of the total) will also change station, therefore moving in a counter-clockwise sense. The result therefore is no net transport of the small macrocycle around the large one.
The only reason there is any net transport initially in this system is because it was constructed so as to have all the rings on one station (i.e. it was statistically imbalanced). It is the restoration of statistical balance which results in net transport. Without the means to regenerate another ‘imbalanced’ situation (e.g. catenane B), no further net transport can occur.
C – The need to break statistical balance (breaking ‘detailed balance’)
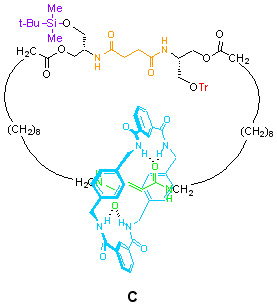
[2]Catenane C combines the elements present in the first two molecules, but now the two stations in the large ring are different and their affinities for the small macrocycle can be switched with an external stimulus creating the required ‘statistical imbalance’ to order. The green station is a fumaramide unit and has much higher affinity for the small ring than the succinamide units used inA and B. This means that even without the gates, the small macrocycle would spend most of its time on the green station.
The fumaramide unit, however, has another trick: irradiate it with light at the correct wavelength (254 nm) and it is converted to its maleamide (cis-olefin) isomer. This unit has a very poor affinity for the small ring compared to the succinamide station. The change is reversible; a number of different stimuli (e.g. catalytic piperidine, bromine radicals (generated by Br2 and white light), or simply elevated temperatures (>100ºC) can bring about the opposite transition, restoring the fumaramide unit. This sequence can therefore repeatedly alter the order of the station binding affinities, switching the preferred position of the small macrocycle from bottom to top and back again: {bottom > top} » {top > bottom} » {bottom > top}……etc.
This provides the essential driving force for repeated net change in position of the small macrocycle (i.e. it gives us control over the thermodynamics of small ring transport). As we have seen with catenane B, the decision of which bulky gate group is removed can be used to select which path the small ring takes each time it moves (i.e. control over the kinetics of small ring transport). By combining these two features in catenane C, we can achieve repetitive unidirectional rotation in either direction simply by carrying out the chemical steps in the correct order (see Scheme 1).
Molecular Motors and the 2nd Law of Thermodynamics
The minimalist design of this system demonstrates the three elements required for directional rotation of submolecular fragment: a randomising element (here, Brownian motion), asymmetry in the dimension of transport (here, variable kinetic barriers) and the breaking of detailed balance (achieved by an energy input). The energetics of such a system are fascinating: 360o rotation of the small macrocycle provides a system identical to the original and formally costs no energy to achieve. Yet, [2]catenane B, illustrates that energy input is required in order to achieve repeated directional motion, as one would expect from the Second Law of Thermodynamics. In other words, although net energy consumption is not required, processing of a particular amount of energy (i.e. you can theoretically get back all you put in, albeit in a different form) is necessary to achieve unidirectional motion with a molecular machine. In [2]catenane C we see that the reason that this is required is to break the statistical balance of the dynamic quantity in the system. Exactly why that is true is one ‘why’ too many for now (and is probably the same reason for which the 2nd Law of Thermodynamics is true), but it does show that no perpetual unidirectionally rotating machine is possible with such a mechanism.
The fact that the sense of rotation – a physical event – is determined solely by the order the chemical reactions are applied in (an external input of information) is also significant. If we combine this idea with the thermodynamic discussion of the previous paragraph we can see that what happens to the small ring in this [2]catenane depends on the interplay between information and energy. The link between information and energy has haunted physics for 150 years (see ‘Maxwell’s Demon’ etc). Learning how to control motion in molecular systems may help to improve our understanding of, and eventually formalise, this relationship.
