Thou Shalt Knot…
‘Tying different knots in a molecular strand’ David A. Leigh, Fredrik Schaufelberger, Lucian Pirvu, Joakim Halldin Stenlid, David P. August and Julien Segard, Nature, 584, 562-568 (2020). Full Article.
In our everyday world strands can be tied into different knots with distinctive properties that can be exploited for different functions, from shoelaces to nooses, hitches, bends and stopper knots.[1] Some of the most advanced equipment ever developed, including the NASA Curiosity Rover used on Mars,[2] use knots to perform key tasks. Although molecular-level knots are found in DNA and proteins,[3] and form at random in polymer chains,[4] to date it has not been possible to tie different types of knots in a particular molecular strand.[5]
Now the Leigh group have developed a way to tie an artificial 15 nanometer molecular strand into any one of several different knots.[6] Biology uses chaperones to direct the folding of peptide chains into the precise 3D structures required of proteins, including examples with knotted architectures.[7] We applied a similar concept to synthetic molecular structures. The key was to intersperse coordination sites for different metal ions along a molecular strand.[8] Selectively activating a set of binding sites causes a ‘tangle’ to form in the thread. Different tangles combine to form larger knots according to mathematical tangle theory (developed by John H. Conway [1937-2020] of ‘Game of life’ fame).[9] In this way, any of three different knots—an unknot (01) macrocycle, a trefoil (31) knot, and a three-twist (52) knot—could be prepared from the same ‘metallo-foldamer’[10] strand by using transition metal and lanthanide ions to guide the molecule through the particular folding and entanglement path chosen.
Tying molecules in knots
If no metal ions are present, cyclisation of ligand L1 forms an unentangled macrocycle (a 01 unknot, Video 1) upon ring-closing olefin metathesis. When foldamer L1 is treated only with LuIII ions, the strand folds into a trefoil (31) knot — a knot with three crossings (Video 2).[11]
Video 1. Cyclisation of 01 unknot macrocycle. [video credit: Stuart Jantzen, www.biocinematics.com].
Video 2. LuIII-template synthesis of 31 trefoil knot. [video credit: Stuart Jantzen, www.biocinematics.com].
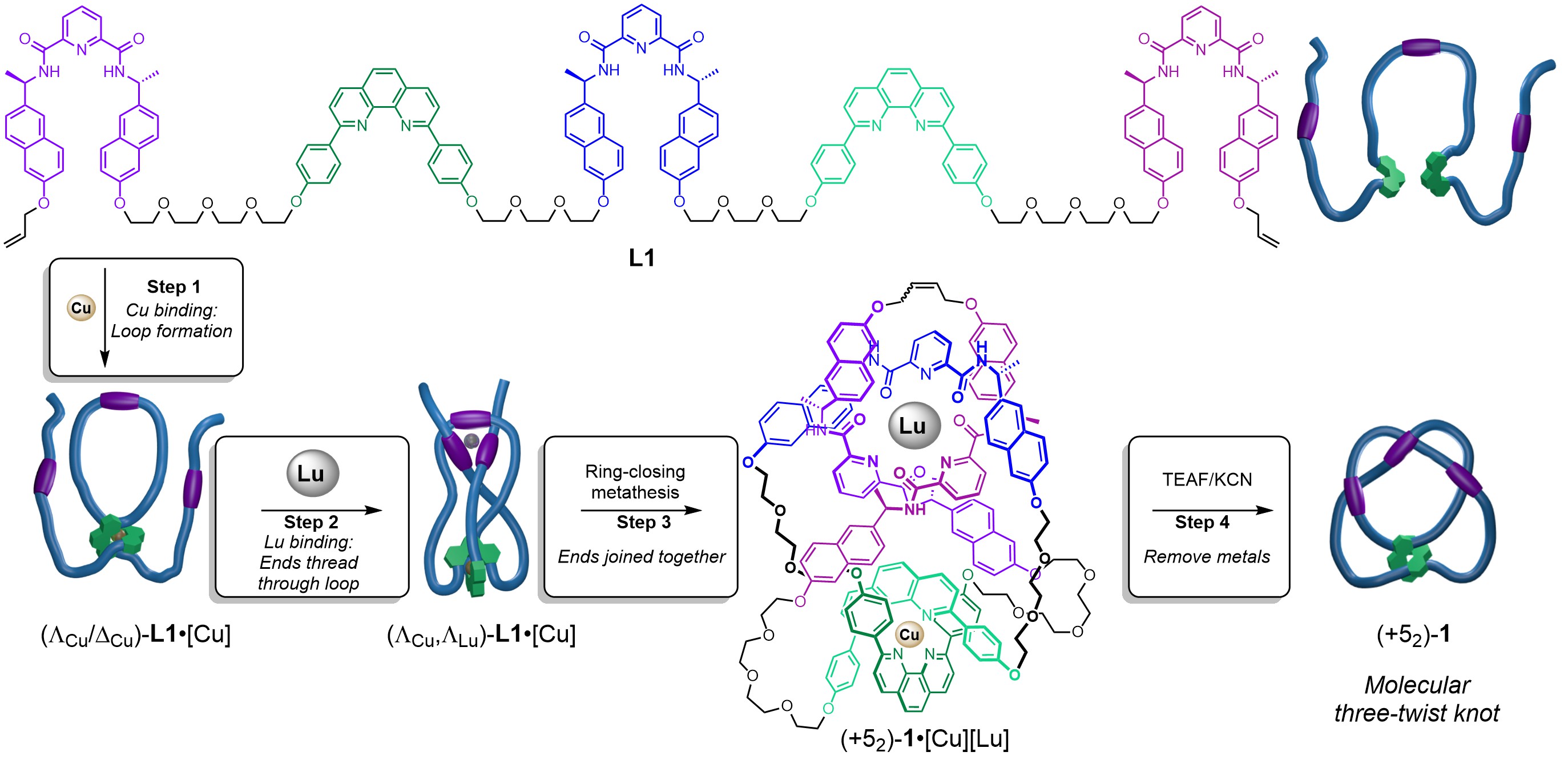
However, when each of the metal binding sites is activated separately, a higher order knot is formed. In the presence of CuI ions foldamer[12] L1 folds to bind the metal ion with the two phenanthroline sites creating an internal loop (Step 1, Figure 1). Subsequent addition of LuIII ions causes the strand ends to thread through the loop from opposite sides so that the three pyridine dicarboxamide units can bind to the lanthanide ion, creating a ‘three-twist knot’ (five-crossing) entanglement in the strand (Step 2, figure 1).[13] A catalyst is then used to join the chain ends in a ring-closing metathesis (RCM), closing the molecular loop and locking in the topology of the 52 knot, (+52)-1•[Cu][Lu] (Step 3, Figure 1). The metal ions that directed the strand folding can then be removed without the knot untying by treatment with F- and CN- (Step 4, Figure 1). The procedure is visualised in Video 3.
Video 3. CuI and LuIII induced folding and entanglement to form 52 knot. [video credit: Stuart Jantzen, www.biocinematics.com].
The metal-ion-induced folding proceeds with stereoinduction: the lanthanide(III)-coordinated tangle can only form with a copper(I)-coordinated tangle of particular handedness. This resembles how one chiral centre can influence the creation of another in conventional asymmetric organic synthesis,[14] but here it applies to the stereochemistry of topological crossings that are not restricted to particular locations in space, rather than to centres or axes of chirality that arise due to the fixed positions of atoms and covalent bonds.
Figure 1. Tying a three-twist knot by programmed folding of a molecular strand.
The three different processes therefore yield (52)-1, (31)-1 and (01)-1, respectively (Figure 2). They are topoisomers: molecules with identical chemical constitution, backbone and atomic connectivity, differing only in the crossing patterns of their entanglements. The different knot isomers have different properties: while the tighter knot (52) can bind two, different, metal ions simultaneously, the looser 31 isomer can only bind either one CuI ion or one LuIII ion.
Figure 2. Three topoisomers generated from the same molecular strand.
Molecular ‘cat’s cradle’
Cat’s cradle[15] is a children’s game that generates different entanglement patterns in a closed loop of string through the players successively manipulating (creating, undoing or changing the position of) strand crossings with their fingers. In an unanticipated development with the 31 trefoil knot, the addition of different metal ions was found to be able to change the position and number of crossings (the writhe) in the non-relaxed form of the molecular closed loop. When CuI was added to (31)-1•[Lu], which has three strand crossing points located at the pyridine dicarboxamide units, the knotted topology prevents both metals being accommodated simultaneously (Figure 3). Instead, the LuIII ion is ejected at the expense of the stronger binding CuI ion. The rearranged structure has four strand crossings: two located near the phenanthroline groups (which bind the CuI ion) and two others which are necessary to twist the trefoil knot into a conformation where the chelating groups can coordinate to CuI (Video 4). The change in writhe (number of crossings) changes the amount of mechanical strain in the structure. It is related to supercoiling in DNA, an important feature of genome packaging, DNA metabolism and gene expression.[3]
Figure 3. Binding different metal ions changes the position of an entanglement within a molecular knot.
Video 4. Molecular cat’s cradle: Changing the crossing positions and writhe in a molecular knot. [video credit: Stuart Jantzen, www.biocinematics.com].
The ability to tie nanoscale strands into different knots, and subsequently change the region and degree of entanglement, opens up new opportunities and new research directions for modifying the function and properties of oligomers, polymers and other synthetic molecular structures.
References
[1] C. Ashley, The Ashley Book of Knots (Doubleday, New York, 1984).
[2] https://www.space.com/17473-ancient-knots-mars-rover-curiosity.html
[3] N. C. H. Lim and S. E. Jackson, ‘Statistical mechanics and topology of polymer chains’, J. Phys.: Condens. Matter 27, 354101 (2015).
[4] M. D. Frank-Kamenetskii, A. V. Lukashin and A. V. Vologodskii, ‘Statistical mechanics and topology of polymer chains’, Nature 258, 398-402 (1975).
[5] a) S. D. P. Fielden, D. A. Leigh, and S. L. Woltering, ‘Molecular knots’, Angew. Chem. Int. Ed. 56, 11166-11194 (2017); b) L. Zhang, J.-F. Lemonnier, A. Acocella, M. Calvaresi, F. Zerbetto and D. A. Leigh, ‘Effects of knot tightness at the molecular level’, Proc. Natl. Acad. Sci. 116, 2452-2457 (2019).
[6] D. A. Leigh, F. Schaufelberger, L. Pirvu, J. Halldin Stenlid, D. P. August and J. Segard, ‘Tying different knots in a molecular strand’, Nature 584, 562-568 (2020).
[7] A. L. Mallam and S. E. Jackson, ’Knot formation in newly translated proteins is spontaneous and accelerated by chaperonins’, Nat. Chem. Biol. 8, 147–153 (2011).
[8] ] J.-F. Ayme, J. E. Beves, C. J. Campbell and D. A. Leigh, ‘Template synthesis of molecular knots’, Chem. Soc. Rev. 42, 1700-1712 (2013).
[9] J. H. Conway, ’An enumeration of knots and links, and some of their algebraic properties’, Computational Problems in Abstract Algebra, (Ed.: Leech, J.), Pergamon Press, Oxford, 329–358 (1970).
[10] G. Maayan and M. Albrecht, (Eds.) Metallofoldamers: Supramolecular architectures from helicates to biomimetics, Wiley-VCH, Weinheim (2013).
[11] (a) C. O. Dietrich-Buchecker and J.-P. Sauvage, ‘A synthetic molecular trefoil knot’, Angew. Chem., Int. Ed. Engl. 28, 189-192 (1989); (b) H. Adams, E. Ashwort, G. A. Breault, J. Guo, C. A. Hunter and P. C. Mayers, ‘Knot tied around an octahedral metal centre’, Nature 411, 763 (2001); (c) P. E. Barran, et al. ‘Active metal template synthesis of a molecular trefoil knot’, Angew. Chem. Int. Ed. 50, 12280–12284 (2011); (d) N. Ponnuswamy, F. B. L. Cougnon, J. M. Clough, G. D. Pantos and J. K. M. Sanders, ‘Discovery of an organic trefoil knot’, Science 338, 783–785 (2012); (e) T. Prakasam, et al. ‘Simultaneous self-assembly of a [2]catenane, a trefoil knot, and a Solomon link from a simple pair of ligands’, Angew. Chem. Int. Ed. 52, 9956–9960 (2013). (f) G. Gil-Ramírez, S. Hoekman, M. O. Kitching, D. A. Leigh, I. Vitorica-Yrezabal and G. Zhang, ‘Tying a molecular overhand knot of single handedness and asymmetric catalysis with the corresponding pseudo-D3-symmetric trefoil knot’, J. Am. Chem. Soc. 138, 13159−13162 (2016); (g) F. B. L. Cougnon, K. Caprice, M. Pupier, A. Bauza and A. Frontera, ‘A strategy to synthesize molecular knots and links using the hydrophobic effect’, J. Am. Chem. Soc. 140, 12442−12450 (2018); (h) Y. Segawa, et al. ‘Topological molecular nanocarbons: All-benzene catenane and trefoil knot’, Science 365, 272–276 (2019).
[12] (a) D. J. Hill, M. J. Mio, R. B. Prince, T. S. Hughes and J. S. Moore, ‘A field guide to foldamers’, Chem. Rev. 101, 3893–4012 (2001); (b) S. Hecht and I. Huc, (Eds.) Foldamers: Structure, properties, and applications. Wiley-VCH, Weinheim (2007); (c) Z. C. Girvin, M. K. Andrews, X. Liu and S. H. Gellman, ‘Foldamer-templated catalysis of macrocycle formation’, Science 366, 1528–1531 (2019).
[13] (a) J.-F. Ayme, J. E. Beves, D. A. Leigh, R. T. McBurney, K. Rissanen and D. Schultz, ‘A synthetic molecular pentafoil knot’, Nat. Chem. 4, 15-20 (2012). (b) V. Marcos, A. J. Stephens, J. Jaramillo-Garcia, A. L. Nussbaumer, S. L. Woltering, A. Valero, J.-F. Lemonnier, I. J. Vitorica-Yrezabal and D. A. Leigh, ‘Allosteric initiation and regulation of catalysis with a molecular knot’, Science 352, 1555-1559 (2016).
[14] R. E. Gawley and J. Aubé, Principles of Asymmetric Synthesis (2nd Edition, Elsevier, New York, 2012).
[15] R. T. Shen and P. G. Wolynes, ‘Statistical mechanics of a cat’s cradle’, New J. Phys. 8, 273 (2006).